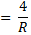Lançamento vertical

Ai vai a resolução de dois problemas que recebi do Alexandre por email...

1. Dois corpos são lançados verticalmente para cima do mesmo ponto com vel. iniciais de 30 m/s. O segundo corpo é lançado 3 s depois do primeiro (g = 10 m/s²). 
a)o instante e a posição do encontro? 
b) as velocidades dos corpos no instante do encontro.


Meu caro Alexandre, em qualquer problema de mecânica, tente equacionar o problema em termos de espaço por tempo, a chamada equação horária do movimento. Isso ajuda muito.


Para o primeiro corpo, sua velocidade inicial é 30 m/s e ele sofre a ação da gravidade. Então sua equação é:


s = s0 + v0.t - 1/2g.t², vamos considerar s0 = 0, o que significa que nossa referência é o ponto de lançamento.


s = 30.t - 5t²


O segundo corpo possui uma equação praticamente idêntica, exceto que seu t é sempre t+3, já que foi lançado 3 segundos depois.


Então 


s = s0 + v0(t+3) - 5.(t+3)², novamente considerando s0 = 0, temos:


s = 30.t + 3.(t + 3) - 5(t² + 6.t + 9) (lembre-se (a+b)² = a² + 2ab + b² ),


s = 30.t  + 3.t - 5.t² - 30.t -45 + 90 


s = 30.t - 30.t + 3.t - 5.t² - 45


s = -5.t² - 45


Igualando as duas equações, temos:


-5t² + 30.t = -5t² - 45


30 t = 45 ; t = 1,5 s !


Neste ponto a velocidade será: v = v0 - at.


v = 30 - 10.(1,5)


v = 15 m/s


(para chegar nessa expressão tem um segredinho. O tempo t=3s não foi escolhido ao acaso, vc pode calcular que neste ponto o objeto está no ponto mais alto e com velocidade zero, então enquanto um acelera para baixo, o outro desacelera para cima.


Substituindo este t = 1,5 s, na expressão horária, temos:


s = 45 - 5(1,5)² = 33,75 m

2. Dois corpos estão na mesma vertical, à distancia de 30 m um do outro. Abandona-se o de cima e, após, 2 s, o outro. Após, quanto tempo e em que ponto se dará o encontro dos dois? (g = 10 m/s²).


A equação horária do primeiro é 


s  = s0 + v0t + 1/2 . g . t² mas vo = 0 e s0 = 0, então,


s = 5t².


Quando o segundo corpo for lançado, o primeiro terá percorrido a distância de:


s = 5(2)² = 20 m


E sua velocidade será:


v = a.t = 10 (2) = 20m/s.


Então podemos reescrever a equação horária do primeiro no momento do lançamento do segundo, assim:


s = s0 + v0t + 1/2 g t² 
s = 20 + 20.t + 5 t²


E a equação horária do segundo objeto fica:


s = 30 + 1/2 g .t² = 30 + 5.t²


Igualando as duas distâncias,


20 + 5.t² = 20 + 20.t + 5t²


     20.t = 10
  
     t=0,5 s


Lembre-se. Isto ocorrerá após os dois segundos em que o primeiro foi lançado. Então o tempo decorrido será de 2,5 s.


s = 30 + 5t² = 30 + 5.(0.5)²


s = 31,25 m


Fiz com um pouco de pressa, posso ter errado alguma coisa, mas conferi varias vezes, se tiver alguma duvida posta ai.


E espero ter colocado ainda a tempo de ser útil...

Busquei ao SENHOR, e ele me respondeu; livrou-me de todos os meus temores. 
Salmos 34:4

Circuitos e Lei de Ohm

Segundo o Google, o assunto mais procurado em meu humilde blog é “Lei de Ohm” e como este assunto é um dos meus preferidos, vou postar a maior quantidade de exercícios que puder a respeito deste.

No exercício abaixo, vou partir do caso mais geral e ir particularizando. O primeiro caso, a menos que você esteja estudando para um curso superior de ciências exatas, você não vai encontrá-lo sob esta forma, mas ai vai...

1.

Encontre o circuito equivalente e a corrente no circuito abaixo, supondo V a ddp (diferença de potencial) entre os terminais A e B.

A manha neste tipo de exercício é encontrar o circuito equivalente. Treine para encontrar um circuito em termos de paralelos e série que seus problemas serão resolvidos.

Veja que na verdade, todos os resistores estão ligados em A e B apenas. Não consegue ver? Tá, vou pintar tudo que está ligado diretamente (curto-circuitado) ao ponto A em vermelho e tudo o que está no ponto B em verde!

Melhor assim?

Então, temos um típico circuito em paralelo de 4 resistores:

Bom, se são resistores em paralelo,

Fácil agora, meu filho?

Pela lei de ohm, V = R.I e se queremos encontrar a corrente I que circula neste circuito,

Eu sei que é obvio, mas não custa nada:

E daí:

(I)


Ou ainda,

Que é a forma geral de 4 resistores ligados em paralelo.

Bien, abaixo uma variação deste exercício:

Caso 2: Em geral este exercício vai ser encontrado assim:

Quatro resistores iguais são ligados como a figura abaixo:

Encontre o valor do resistor equivalente e a corrente elétrica no circuito.

Já tá colorido para o caso de você ter pulado a primeira parte. Então, os quatro resistores estão na verdade estão em paralelissimo, ficando assim:

Da expressão (I) quando R=R1=R2=R3=R4, temos:

E Req

Muito bem, mas se você é um ser normal que não vai cursar engenharia, física, matemática e outras loucuras, o exercício abaixo é pra você, mas leia os anteriores que uma coisa depende da outra:

Suponha quatro resistores de 100 ohms ligados como a figura abaixo. Encontre o valor da resistência equivalente entre A e B.

Então, de novo, o pulo do gato é ver que este circuito é um circuito paralelo puro e simples, vendo isso fica muito fácil:

Existem maneiras de incluir um resistor ai e deixar a coisa ficar bem mais complicada, mas isso fica para outro POST.

Não percam as grandes aventuras da Lei de Ohm na Internet...

Porque para mim tenho por certo que as aflições deste tempo presente não são para comparar com a glória que em nós há de ser revelada. 
Romanos 8:18