Mais força G !

Esta é uma homenagem ao narrador da prova de Stock Cars, transmitida ontem pela Globo, no horário do Globo-esporte que dizia que tinha um mostrador da “Força da Gravidade”. Não meu filho, não. Se lesse meu Blog não falava besteria. Este POST está pronto desde sabado, mas só foi possível colocar no ar agora.

Mas vamos a um pouco de teoria, que não faz mal pra ninguém.

O problema é o seguinte: Calcule o módulo da aceleração de um móvel, preso a uma corda de raio R, girando num período constante T.

A primeira vista a resposta é fácil, se o período é constante, então a velocidade é constante e portanto não há aceleração, certo ? Muito bem. Errado !

Errado porque, apesar do módulo da velocidade ser constante, de fato, o vetor velocidade muda de direção a todo instante e se mudou, acelerou !

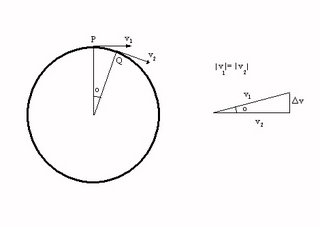Muito bem. Na figura ao lado, tem um desenho do movimento (acho que pra ver melhor é preciso dar um click nela). Inicialmente vamos considerar que a velocidade do móvel é v1 no ponto P e v2 no ponto Q. Sabemos que ambos os vetores tem mesmo módulo e vamos supor que entre o ponto P e Q, o ângulo formado entre o centro da circuferência (vamos chamar de O) P e Q é o (deveria ser a letra grega teta minúscula, como nos livros conceituados, mas como não faço a mínima idéia de como fazer letra grega no Blog e este também não é, ainda, um Blog conceituado, vai ser "o" mesmo.

É bom lembrar que o deve ser um ângulo pequeno. Por exemplo quarenta e cinco graus já não fica muito bom.

Bem, voltando. O vetor velocidade é sempre tangencial a circunferência. Assim, o ângulo o entre OP e OQ também é o ângulo entre v₁ e v₂.

Pô, isso é bom, não é ? Semelhança de triângulos ajuda muito na hora de resolver problemas. Como o que nos interessa é a variação de velocidade delta v (outra vez, problemas ao encontrar caracteres gregos, esses gregos, parece que não tinham Internet). Mas pela semelhança dos triângulos, a relação:



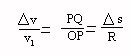
Que podemos rearranjar para:



Muito bem. Como o que queremos encontrar é a aceleração e esta é a relação entre a variação de velocidade e um determinado espaço de tempo, temos:

No limite, quando delta t tender a zero (não sabe limite ? Ô cuitado !!!! Um dia você aprende. Talvez eu poste aqui alguns conceitos, não perca !), temos:

Esta é a expressão que pode ser usada em milhares de problemas. Mas o que fornecemos não foi a velocidade e sim o período de revolução. Ora relampagos. Se o perímetro da circunferência é dado por 2 . pi . R, então nosso v é isso aí dividido por T. O que temos finalmente:

Muito bem. Temos a aceleração causada pela força centripeta (para o centro). Se quiser saber a intensidade desta força é só multiplicar pela massa do objeto.

A tal da Força G tem modulo igual a esta força, porém sentido contrário (centrifuga ou fugindo do centro). Como já comentei outro dia, essa força de fato não existe. É a sensação que alguém que estivesse solto dentro de nosso objeto rodante (rodante é bonito demais, agora alem de fisico virei criador de palavras, o que o poder faz com o cidadão) sentiria contra o piso em função da Inércia querer levar o nosso alguém a continuar em linha reta (em direção ao v1 ou v2 no desenho lá de cima).

Este exercício é difícil para estudantes de nível médio, mas é entendível. Amanhã vou tentar colocar uns números nele pra ficar mais simpático.

(Fala sério, uma formula com pi é simbolo de nerdisse... Aquele program Mythbuster - que eu adoro - já abre com uma formula envolvendo pi...)